Collisions With VPython Student Guide
Table of contents
In this exercise we will investigate elastic and inelastic collisions.
- There are questions asked of you throughout this assignment, labeled Question 1, Question 2, etc. Write down the answers in the TERM booklet (to be handed in at the end of the Practical).
- At the end of the Practical, hand in your TERM booklet, along with a printed copy of your code for the final exercise (collisionexC.py). Please staple the code into the booklet.
- If you are working with a partner, the two of you must reach a consensus about an answer before moving on to the next part. Feel free to ask the TA for help if a consensus cannot be reached.
- All quantities are in SI units; distance in meters (m), time in seconds (s), velocity in m/s, acceleration in m/s2, and mass in kg.
If we consider a system of 2 particles with no external forces acting, then the momentum of the system must be conserved. If the particles collide, then the total momentum of the system after the collision must equal the total momentum of the system before the collision.
All collisions will conserve momentum. Elastic collisions also conserve kinetic energy. Totally inelastic collisions lose the maximum possible kinetic energy. Most collisions are inelastic, where some kinetic energy is lost, but not the maximum possible.
Which type of collision occurs depends on the material of the colliding objects and other conditions. For example, two billiard balls colliding will be very different from two balls of Velcro.
 Exercise A: Totally Inelastic Collisions
Exercise A: Totally Inelastic Collisions
In “Totally inelastic collisions” the particles completely stick together after the collision. This means their velocities after the collision are the same.

Download the program collisionexA.py and save it on your computer. This program is not complete, so if you try to run it you will get a “syntax error” – see the steps below to fix it. The goal of the program is to create and display 2 balls with masses m1 and m2 and initial constant velocities v1 and v2. The positions of the balls are updated in the while loop. When the balls collide, the velocities need to be changed. This is done in the “if” conditional which is supposed to check that the balls have collided, and if so, changes the velocities of both balls.



- m1 = m2
- m1 > m2
- m1 < m2
- m1 >> m2
- m2 >> m1
 Exercise B: Elastic Collisions
Exercise B: Elastic Collisions
The other extreme in collisions is an “elastic collision”. In this case, kinetic energy is conserved. We can’t use the constraint that \(\vec{v}_2=\vec{v}_1\) after the collision so we need another piece of information to find the velocities of the 2 balls after the collision.

Save a new copy of the .py file you had at the end of Exercise A, call it “collisionexB.py”. Replace the two lines under the comment “#Update the post-collision velocities” with the following:
v1final= ??
v2final= ??
v1=v1final
v2=v2final
Note that we calculated the final velocities first before updating v1 and v2 values.

Run your program.


- m1=m2
- m1 > m2
- m1 < m2
- m1 >> m2
- m1 << m2
 Exercise C: Elastic Collisions in Two Dimensions
Exercise C: Elastic Collisions in Two Dimensions
For an elastic collision in two dimensions we have three conservation equations from the bottom of page 156 of Wolfson:
\(\begin{eqnarray} m_1 v_{1{\rm i}x} + m_2 v_{2{\rm i}x} = m_1 v_{1{\rm f}x} + m_2 v_{2{\rm f}x} \end{eqnarray}\) (C1. Conservation of x-component of momentum)
\(\begin{eqnarray} m_1 v_{1{\rm i}y} + m_2 v_{2{\rm i}y} = m_1 v_{1{\rm f}y} + m_2 v_{2{\rm f}y} \end{eqnarray}\) (C2. Conservation of y-componentof momentum)
\(\begin{eqnarray} \frac{1}{2}m_1 v_{1{\rm i}}^2 + \frac{1}{2}m_2 v_{2{\rm i}}^2 = \frac{1}{2}m_1 v_{1{\rm f}}^2 + \frac{1}{2}m_2 v_{2{\rm f}}^2 \end{eqnarray}\) (C3. Conservation of kinetic energy)
To solve problems, let's start in the rest-frame of ball 2, so that \(\vec{v}_{2{\rm i}} = 0\). Also, let's rotate our reference frame so that, initially, ball 1 travels in the +x-direction, so that \(v_{1{\rm i}y} = 0\). We can write the initial x-component of the velocity of ball 1 simply as v1i. The conservation equations are simplified somewhat to be:
\(\begin{eqnarray} m_1 v_{1{\rm i}} = m_1 v_{1{\rm f}x} + m_2 v_{2{\rm f}x} \end{eqnarray}\) (C4)
\(\begin{eqnarray} m_1 v_{1{\rm f}y} = -m_2 v_{2{\rm f}y} \end{eqnarray}\) (C5)
\(\begin{eqnarray} \frac{1}{2}m_1 v_{1{\rm i}}^2 = \frac{1}{2}m_1 v_{1{\rm f}}^2 + \frac{1}{2}m_2 v_{2{\rm f}}^2 \end{eqnarray}\) (C6)
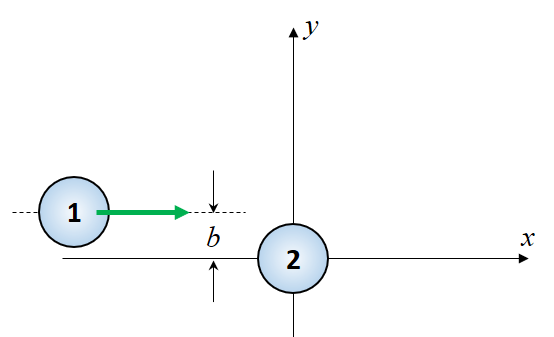
Let's place the centre of ball 2 at the origin. Define the impact parameter, b, as the initial y-position of the centre of ball 1.
Figure C1: Before Collision
Next, let's make the assumption for this part that both balls have equal mass, m1 = m2 = m. Then the conservation equations become:
\(\begin{eqnarray} v_{1{\rm i}} = v_{1{\rm f}x} + v_{2{\rm f}x} \end{eqnarray}\) (C7)
\(\begin{eqnarray} v_{1{\rm f}y} = -v_{2{\rm f}y} \end{eqnarray}\) (C8)
\(\begin{eqnarray} v_{1{\rm i}}^2 = v_{1{\rm f}}^2 + v_{2{\rm f}}^2 \end{eqnarray}\) (C9)
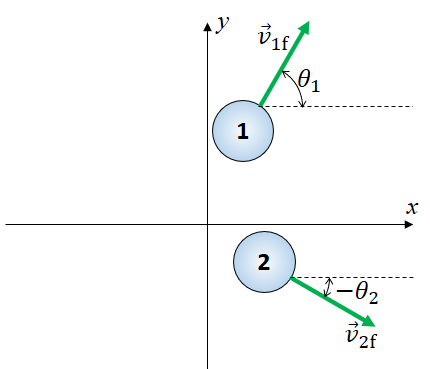
Lastly, let's define \(\theta_1\) to be the angle of the final velocity of ball 1 with respect to the x-axis, and \(\theta_2\) to be the angle of the final velocity of ball 2 with respect to the x-axis. In both cases, we use the convention that positive angles are measured counterclockwise with respect to the x-axis. Therefore \(\theta_2\) is a negative number.
Figure C2: After Collision
The conservation equations then become:
\(\begin{eqnarray} v_{1{\rm i}} = v_{1{\rm f}}\cos\theta_1 + v_{2{\rm f}}\cos\theta_2 \end{eqnarray}\) (C10)
\(\begin{eqnarray} v_{1{\rm f}}\sin\theta_1 = -v_{2{\rm f}}\sin\theta_2 \end{eqnarray}\) (C11)
\(\begin{eqnarray} v_{1{\rm i}}^2 = v_{1{\rm f}}^2 + v_{2{\rm f}}^2 \end{eqnarray}\) (C12)
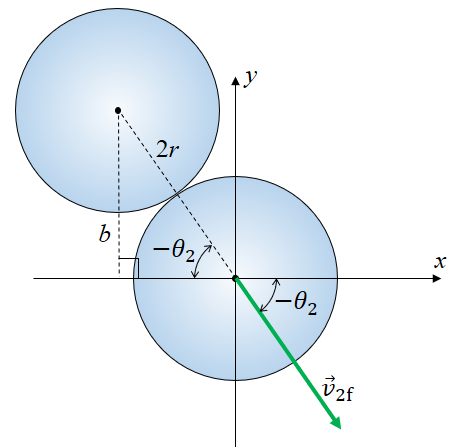
It can be shown that for balls of equal mass, \(\theta_1 - \theta_2 = 90^\circ\). (See Wolfson Example 9.11, and Problem 9.72.). If the balls are spheres and are quite rigid, then the collision is very short, and during the collision, the normal force of ball 1 on ball 2 is the only force which accelerates ball 2 from rest. Therefore, the final velocity of ball 2 can be found from the geometry of the collision itself, shown in Figure C3.
Figure C3: During Collision. Note that the balls only will collide if b < 2r.
To Do: Save a new copy of the .py file you had at the end of Exercise B, call it “collisionexC.py”. For purposes of checking the initial and final momentum and energy, set the masses of the two balls equal to 1 kg. Under the lines to set the radius of the balls, Set the impact parameter [in m] to be b = 0.2.





v1final=vector(v1fmag*cos(theta1),v1fmag*sin(theta1),0)
v2final=vector(v2fmag*cos(theta2),v2fmag*sin(theta2),0)
Check your code, and see if it does what you expect for various values of b. Write down the final velocities for the following impact parameters:
- b = r/2
- b = r
- b = 3r/2.

What if the balls are not the same mass? How would you modify the code to account for this?
[Note: This Module was written by Omar Gamel in September 2014, based on activities written by Sabine Stanley 2010-2014.]