Conical Pendulum At Home

Goal

Use the Tracker Software to analyze the motion of a conical pendulum, as viewed from the side.

Background

To quote https://en.wikipedia.org/wiki/Conical_pendulum :

"A conical pendulum consists of a weight (or bob) fixed on the end of a string or rod suspended from a pivot. Its construction is similar to an ordinary pendulum; however, instead of swinging back and forth, the bob of a conical pendulum moves at a constant speed in a circle with the string (or rod) tracing out a cone. The conical pendulum was first studied by the English scientist Robert Hooke around 1660 as a model for the orbital motion of planets."

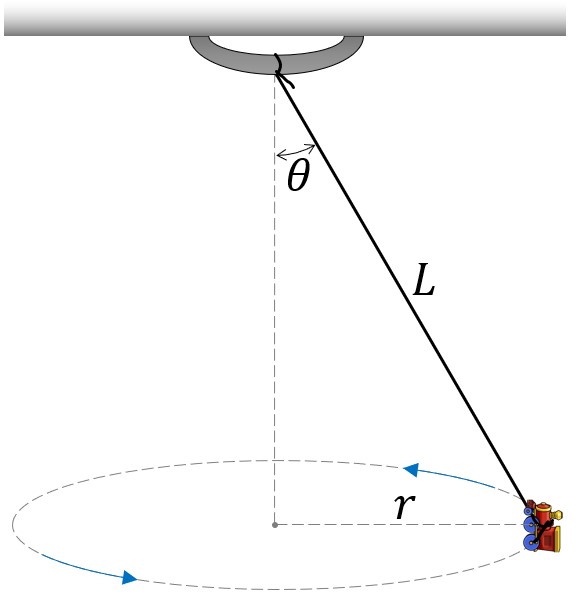
Activity

Construct a conical pendulum in your house.  You will need some string.  Tie one end of the string to a small heavy object.  Tie the other end of the string to some fixed, elevated point under which you can make the object swing in a horizontal circle.  Record the length L, between the fixed point where you tied the string to the centre of mass of the swinging object.

Set the object traveling in a horizontal circular motion at a constant angle \(\theta\) , as measured outward from when the object hangs straight down.  Take a video of the motion as viewed from the side.  Make sure the frame includes the entire pendulum, including the fixed point at the top.   Take the video for 2 or 3 complete circles.

Load the video into Tracker.  In order to calibrate the distance scale, play the video until the pendulum seems to be the furthest to the left or right.  At this moment, pause the video and add a calibration stick which is the length of the string, L, that you measured before.  Click Create and add a Point Mass.  Frame by frame, press shift while you click the mouse button to add position-time measurements for the pendulum as it travels in a horizontal circular path.  Since you are viewing the motion from the side, it will appear just to go back and forth.

Include all details of your methods in your presentation, including photos of your apparatus, and screen-shots showing the trajectory with positions from frames marked.

NOTE: Each pod member in your pod should provide a video for analysis to go into your Google slides.  Choose the best or most interesting video analysis for presentation to the group during your Practical time.

Analysis

Question 1.  From your video data, estimate the radius of the circular motion, r. How did you find this radius, and what is the uncertainty?  Is this radius constant throughout the motion in your video, or does it change?

Question 2.  From your video data, estimate the angle, \(\theta\), of the motion.  How did you find this angle, and what is the uncertainty?  Is this angle constant throughout the motion in your video, or does it change?

Question 3.  From your video data, estimate the speed, v, of the motion.  How did you find this speed, and what is the uncertainty?  Is this speed constant throughout the motion in your video, or does it change?  Can you think of any reasons why you might expect the speed to change with time?

Question 4.  [Theory]  Either on paper, or using a tablet, show that, for a conical pendulum, the speed is related to the radius and angle by the following equation:

\(v = \sqrt{gr \tan \theta }\)

where g = 9.80 m/s² is the acceleration due to gravity.  Be sure to include your derivation in your presentation. 

Question 5. From your measurement of r and \(\theta\) from questions 1 and 2, and your theoretical relation from question 4, what is your predicted value for the speed?  How does that compare with the measured value in Question 3?