Mechanics Module 6 Pandemic Version
Table of contents
 Activity 1
Activity 1
The figure below shows four cases of point particles in uniform circular motion: A, B, C, and D. The motion of all four masses are in the horizontal plane. Recall that for a point particle of mass m moving with speed v in a circle of radius r the angular momentum:
\(L=mvr\)
-
Rank in order from the largest to the smallest the angular momentum L of the four cases. Explain your reasoning.
-
Recall that for an object in circular motion with radius r and speed v, the angular velocity \(\omega\) is defined as: \(\omega = v/r\). Rank in order from the largest to the smallest the angular speed of the four cases. Explain your reasoning.
 Activity 2
Activity 2
The four masses of Activity 1 have been connected to a massless frame that is rotating in the horizontal plane about the central pivot point, as shown. The “spokes” of the frame are rigid.
-
Will the motions of the masses tend to distort the frame in the horizontal plane?
-
What is the total angular momentum of the four masses?
-
What is the rotational inertia of the combined system of four masses?
-
Compare the results for using the equation \(L = mvr\) for the four individual point masses and adding them up, versus using \(L = I \omega\) for the whole object.
 Activity 3
Activity 3
Take an object and tie it to a string. This may be the same object you used for a conical pendulum in a previous week's activity. Thread the string through a drinking straw. Hold the straw in one hand, and whirl the object in a horizontal circle, being careful not to hit anything or anyone with it. Keep the string below the straw taut with your other hand. If you make the axis of rotation directly over your head you will be much less likely to hit yourself in the head with the object. [NOTE: If you cannot find the materials to do this experiment, there is a video of Professor Harlow trying it in the Pre-Practicals Video this week.]
Uniform Circular Motion
-
Is the linear momentum \(\vec{p} = m \vec{v} \) of the object conserved as the object moves in uniform circular motion? Explain.
-
Is the kinetic energy ½ mv2 of the object conserved as the object moves in uniform circular motion?
-
Is the angular momentum of the object, \(\vec{L}=\vec{r} \times \vec{p}=mr^2 \vec{\omega}\), conserved as the object moves in uniform circular motion?
Decreasing the Radius of the Circular Motion by pulling the string
-
Whirl the object again in a horizontal circle. Reduce the radius r of the circle to about ½ r by pulling on the string hanging below your hand. What happens to the speed of the object when you do this?
-
Do you think the kinetic energy was conserved as the radius of the circle was being reduced? Explain.
-
Do you think the angular momentum was conserved as the radius of the circle was being reduced? Explain.
-
If the speed of the object was v when the radius of the circle was r, what do you predict was the speed when the radius of the circle was ½ r? If the magnitude of the angular velocity of the object was \(\omega\) when the radius of the circle was r, what was its magnitude when the radius of the circle was ½ r?
 Activity 4
Activity 4
-
Here is a figure of a yoyo that is in free fall: the string is not attached to anything and is not shown in the figure. Draw a free body diagram of the forces acting on the yoyo. Assume that air resistance in negligible.
-
Here is a cross section of a yoyo that is falling with the end of the string fixed to a support. In Part A, you could reasonably assume that the yoyo is a point particle. The free body diagram for this case must treat the yoyo as an extended body, and where the forces are exerted on it is important. Draw an extended free body diagram of the forces acting on the yoyo.
-
If both yoyos are released at the same time from the same height do they both fall at the same rate? Which moves fastest? If you have a yoyo, confirm your prediction by dropping the yoyo with and without you holding the string. Or you can drop it side-by-side with an object of similar size.
-
Explain the results of Part C qualitatively using Newton’s Laws.
-
For both yoyos, does the force of gravity of the Earth do any work on the yoyo? If so, does the force of gravity do positive work or negative work on each yoyo? Explain.
-
For the yoyo of Part B, does the force exerted on the yoyo by the string do any work on it? If so, does the string do positive work or negative work on the yoyo? Explain.
 Activity 5
Activity 5
For this activity it is important to remember that, at all times, the yo-yo is not supposed to slip. It can roll, but it cannot slide. Please ask your TA about this distinction if it does not make sense.
-
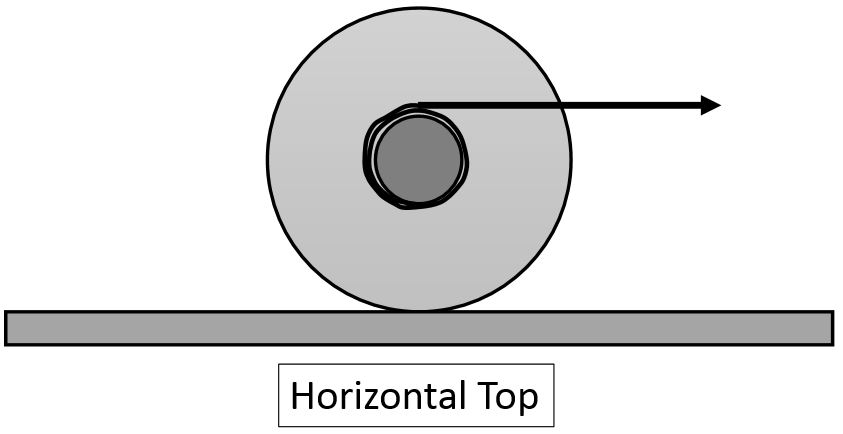
A yoyo sits on the tabletop, and is gently pulled to the right by the horizontal string, which is wound about the axel clockwise as shown in the cross-section view. The pull is gentle enough that the yoyo does not slip. Predict the motion of the yoyo. If you have a yoyo, check your prediction. If not, refer to the Pre-Practical video for this week. Did you predict the sense of the rotation correctly?
-
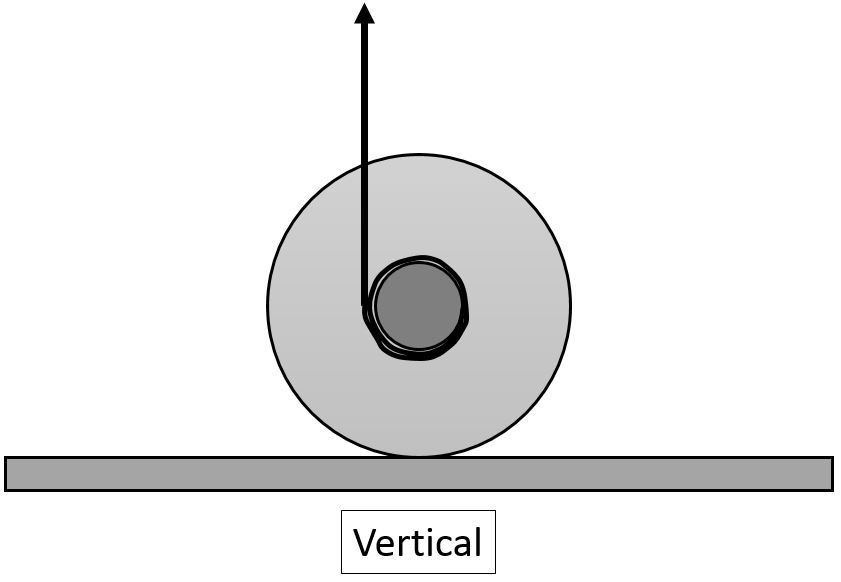
A yoyo sits on the tabletop, and is gently pulled upward by the vertical string, which is wound about the axel clockwise as shown in the cross-section view. The pull is gentle enough that the yoyo does not slip. Predict the motion of the yoyo. If you have a yoyo, check your prediction. If not, refer to the Pre-Practical video for this week. Did you predict the sense of the rotation correctly?
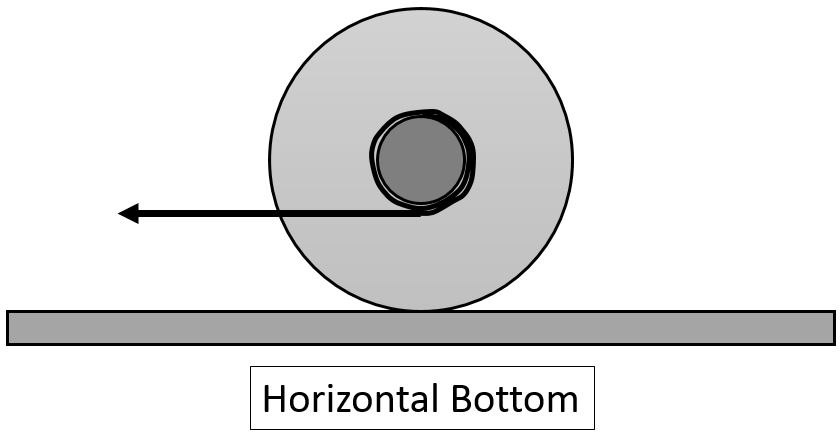
- A yoyo sits on the tabletop, and is gently pulled to the left by the horizontal string, which is wound about the axel clockwise as shown in the cross-section view. The pull is gentle enough that the yoyo does not slip. Predict the motion of the yoyo. If you have a yoyo, check your prediction. If not, refer to the Pre-Practical video for this week. Did you predict the sense of the rotation correctly?
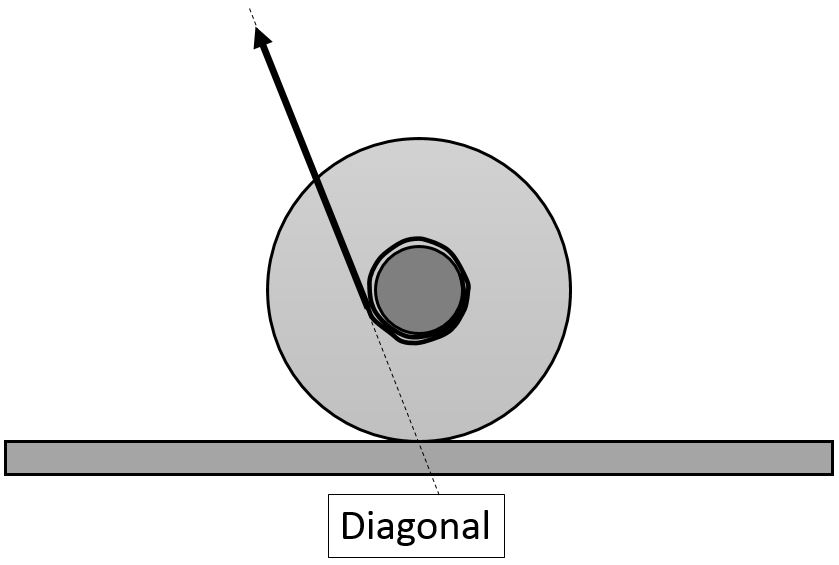
- A yoyo sits on the tabletop, and is gently pulled along a diagonal by a string which is wound about the axel clockwise as shown in the cross-section view. The pull is gentle enough that the yoyo does not slip. Predict the motion of the yoyo. If you have a yoyo, check your prediction. If not, refer to the Pre-Practical video for this week. Did you predict the sense of the rotation correctly?
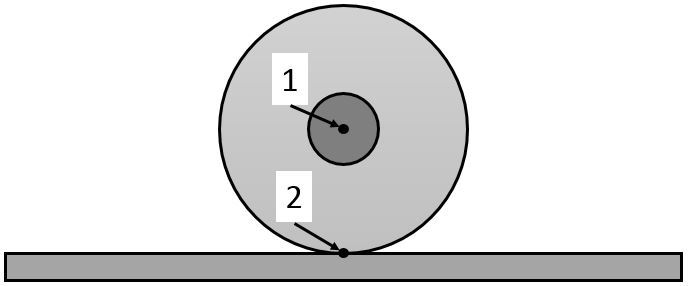
- Consider the torque on the yoyo due to the tension in the string. Before you can calculate torque, you must choose a rotation axis. The figure below shows two possible choices: 1. centre of yoyo, or 2, bottom of yoyo where it touches the horizontal surface. For each of the configurations in Parts A-D, determine the sense (clockwise or counterclockwise) of the torque about points 1 and 2. You may wish to tabulate your data for the eight different torques. Add to your table the observed actual rotation of the yoyo when these four configurations were tested. Based on the observations, is it better to say the yoyo rotates about point 1 or point 2?
Draw an extended free body diagram of the yoyo for configuration D and use that to explain the motion of the yoyo for different angles of the diagonal.
The original version of this guide was written in May 2008 by David M. Harrison, Dept. of Physics, Univ. of Toronto Activity 11 is from Tutorials in Introductory Physics by Lillian C. McDermott, Peter S. Shaffer ©2002 by Prentice-Hall, Inc.