Mechanics Module 5 Student Guide

   Activity 1

Two balls are launched with equal initial speeds along tracks as shown. Friction and air resistance are negligible.

1. Predict which ball reaches the end of its track first.

2. You may check your prediction with a Flash animation at:

http://uoft.me/HFMRacingBalls

A similar situation for skiers instead of balls is at:

http://uoft.me/HFMRacingSkiers

Of course, with animations one may program the wrong answer. To watch a slow-motion video of a real apparatus, click here.  (Video courtesy of the University of Maryland Department of Physics http://lecdem.physics.umd.edu/c/c2/c2-11.html )

Was your prediction correct?

3. Qualitatively explain the results of the race using conservation of energy

4. Qualitatively explain the results of the race using forces and accelerations.

 

    Activity 2

Skills used in this activity. Force Diagram. Able to use representations to solve problems. Able to make a reasonable prediction based on a hypothesis.

In Mechanics Module 3 Activity 11 you may have whirled a ball on a string in a vertical circle and noted that the speed of the ball at the bottom of the circle is greater than the speed at the top. At that time we did not explore why this is so very carefully.

1. Qualitatively explain the difference in the speeds using conservation of energy and energy bar charts.

2. Qualitatively explain the difference in the speeds using tangential forces and tangential acceleration.

 

    Activity 3

 

Skills used in this activity. Extract information from representation. Able to use representations to solve problems. Able to identify the assumptions making the prediction. Able to make a reasonable prediction based on a hypothesis.

Three balls are the same height h above the ground and are fired with the same initial speeds v₀. Ball A is fired straight up, ball B is fired horizontally, and ball C is fired straight down. Air resistance is negligible.

 

1. Rank the speeds, from the largest to the smallest, of the three balls when they hit the ground. Explain.

2. Rank the time, from the largest to the smallest, it takes the three balls to hit the ground. Explain.

 

    Activity 4

 

Joe is standing on the ground, Peter is standing on a 10 m high cliff, and Amanda is at the bottom of a 20 m deep pit, as shown. All three are using coordinate systems with the vertical axis directed up.

Joe’s coordinate system has the zero of the vertical axis at ground level.

Peter’s coordinate system has the zero of the vertical axis at the height of the cliff.

Amanda’s coordinate system has the zero of the vertical axis at the bottom of the pit.

A ball of mass m is initially at rest at ground level, Position A above the pit.

1. What is the gravitational potential energy of the ball for Joe, for Peter, and for Amanda?

2. The ball is then raised to the height of the cliff, Position B, and is held at rest. What is the gravitational potential energy of the ball at Position B for Joe, for Peter, and for Amanda?

3. The ball is then released from rest and strikes the ground at the bottom of the pit, Position C. What is the gravitational potential energy of the ball at Position C for Joe, for Peter, and for Amanda?

4. What is the speed of the ball at Position C for Joe, for Peter, and for Amanda?
    

---

The following is used in Activities 5 - 8

A horizontal spring has an equilibrium position \(x_0\). When the mass \(m\) is at position \(x_0\) as shown the spring exerts no force on it. When the spring is either stretched or compressed, the position of the mass is \(x\), so the displacement of the mass from the equilibrium position is \((x-x_0)\) and the force the spring exerts on the mass is:

\(F=-k(x-x_0)\)

We assume an ideal spring and negligible air resistance, and define the system to be the spring and the mass. At any instant in time, the total mechanical energy of the system is the kinetic energy of the mass plus the potential energy of the spring. The mechanical energy is equal to:

\(E={1 \over 2}m v^2 + {1 \over 2} k (x - x_0)^2\)

---

 

    Activity 5

Note: Just before Activity 5 there is a picture of a horizontal spring-and-mass system with some equations. This is useful to read before doing this activity.

In the above figure we have chosen a coordinate system that points from the right to the left.

1. For values of x > x₀ does the force point in the +x or the –x direction?

2. For values of 0 < x < x₀ does the force point in the +x or the –x direction?

3. For values of x < 0 does the force point in the +x or the –x direction?

 

   Activity 6

Note: Just before Activity 5 there is a picture of a horizontal spring-and-mass system with some equations. This is useful to read before doing this activity.

1. The term  ​\({1 \over 2} k (x - x_0)^2\)​ is the elastic potential energy of the spring. Explain in your own words where the ​\({1 \over 2}\)​  term comes from. There are at least two ways that you may wish to think about this.
2. In a graph of the force versus the distance, what physical quantity is given by the area under the graph?
3. When you stretch a spring from initial length x₁ to final length x₂, what physically is \(\begin{eqnarray} \int_{x_1}^{x_2} F dx \end{eqnarray}\)? 

 

    Activity 7

Note: Just before Activity 5 there is a picture of a horizontal spring-and-mass system with some equations. This is useful to read before doing this activity.

The same spring as is used in Activity 5 is now suspended vertically. You may wish to note that the coordinate axis is now labeled y, while in the introduction above it was labeled x. The position labeled x₀ to the right is the same equilibrium position of the spring as before. For the purpose of this question, your hand is never touching the spring-and-mass system, so do not include it in any free body diagrams.

Note: x₀ is just a label. Feel free to call it y₁ if that makes things easier for you to understand.

 

1. If the mass is at position x₀, the equilibrium position of the spring, draw the free body diagram of the forces acting on the mass.

2. At position x₀, what is the net force acting on the mass?

3. If the mass is at some position y₀, the net force on the mass is zero. Draw the free body diagram of the forces acting on the mass.
   (We will call y₀ the equilibrium position of the mass on the spring.)

4. Derive the expression for y₀ in terms of m, g, k, and x₀? 

5. Derive the net force acting on the mass as a function of k, y, and y₀? First find the general expression for the net force at any position y, then eliminate x₀ by using your answer from part D.

6. What is the total mechanical energy (kinetic energy plus potential energy) when the mass is oscillating in terms of k, y, and y₀, as well as m and v? 

7. Draw an energy-position graph with energy on the y-axis and position on the x-axis. Include the gravitational potential energy, the spring potential energy, and the total potential energy (spring + gravity). Make sure you clearly label the three energies. Also label the locations x₀ and y₀ and discuss the significance of these locations in terms of the three functions (potential energies) you drew.

8. On the Moon, gravity is about one sixth as strong as on Earth. If you moved your mass-and-spring system to the Moon, what would happen to the values of x₀ and y₀?

 

  Activity 8

Note: Just before Activity 5 there is a picture of a horizontal spring-and-mass system with some equations. This is useful to read before doing this activity. Further, this activity assumes you have done the previous activity. If you have forgotten what any of the variables represent, please go back and reread the previous activity.

This activity uses the Motion Sensor.  To access the software, click on the Start button, then click on Labview Shortcuts.  Double-click the "Motion Sensor" item to start the software. You can read more about how the detector works at http://www.upscale.utoronto.ca/Practicals/Manuals/Equipment/MotionSensor/MotionSensor.pdf

Suspend the supplied mass from the supplied spring. Gently lift the mass a small amount and release it, so that it bobs up and down. The oscillations should be small enough so that the motion is smooth and the spring is always vertical and stretched. Place the Motion Sensor under the mass with the transducer pointing up so it tracks the position of the mass. Later we will learn how to describe the distance as a function of time. Here we will begin to explore oscillatory motion and look at the total mechanical energy of the system.

Collect distance-time data for the mass when it is vertically oscillating. Be aware that the Motion Sensor has a switch which adjusts the width of the beam; one of the switch settings will probably result in better data than the other. Recall that the Motion Sensor can only measure distances greater than 0.15 m. This means that for the coordinate system of Activity 7, if the Motion Sensor is at y = 0 the bottom of the mass must always have a value of y > 0.15m.

• Set the vertical position of the mass-spring position so that when the mass is oscillating the minimum distance from the Motion Sensor is close to but greater than 0.15 m. Try to have the mass moving only up and down.

• Set the Motion Sensor for the wide beam. On some units this is indicated by an icon of a person.

• After starting the Motion Sensor software, set the sample rate to about 60 samples per second. You may wish to try a different sampling rate to see if it improves the quality of your data.

• Collect data for just a few oscillations.

Here are some tips for analyzing your data:

• It is likely that there will be noise in your values of the distance. These propagate to even greater noise in the displacement, velocity and acceleration. Use the cursors in the main Distance-Sample plot to select a reasonably clean set of data encompassing at least a bit more than half of one complete oscillation. The velocity-time graph is often particularly useful in determining the “region of interest” that you wish to keep. Sometimes the data will be so noisy that it is a good idea to take another set.

• The acceleration plot will be particularly noisy. By default this plot displays all of the values. You can adjust the minimum and maximum values of the plot to show the main features of the data without showing any noisy values by double-clicking on the minimum or maximum value of the vertical axis, putting in a new value, and pressing Return on the keyboard.

Now the Activities:

1. From your data, what is the value of y₀ (the distance from the sensor to the equilibrium position of the mass on the spring)?

2. When the mass is at y₀, is its speed a maximum or a minimum?

3. What is the value of the speed when the mass is at y₀? Try to account for the noise in the plot by assigning an uncertainty to the value.

4. When the mass is at y₀, is the magnitude of its acceleration a maximum or a minimum?

5. When the mass is at y₀ what is the value of its acceleration? Try to account for the noise by assigning an uncertainty to the value.

6. From your data what is the maximum displacement of the mass from its equilibrium position (also called the "amplitude" of the oscillation)? When the mass is at this position, is its speed a maximum or a minimum?

7. What is the value of the speed when the mass is at its maximum displacement? What is the uncertainty in this value?

8. When the mass is at its maximum displacement is its acceleration (let's consider its absolute value here) a maximum or a minimum?

9. What is the value for the spring constant k and the uncertainty in this value?

10. During the oscillation, when the mass is at y₀ what is the total mechanical energy? When the mass is it its maximum displacement what is the total mechanical energy? From your data is mechanical energy conserved within your estimated uncertainty? Explain.

 

 

    Activity 9

For an ideal spring-mass system we may write Newton’s 2^nd Law as:

\(F = -k x = ma\)       (9.1)

If one knows integral calculus then Eqn. 9.1 can be integrated to show that the mechanical energy E_mech is conserved, where:

\(E_{\rm mech}=\frac{1}{2}mv^2+\frac{1}{2}kx^2\)       (9.2)

In fact, integral calculus was invented by Newton (and independently by Leibniz) to do just this sort of Physics calculation.

Here you will use only dimensional and unit analysis, Newton’s 2^nd law, and the calculus of derivatives to show the relation between these equations.

Let us assume that the elastic potential energy U_s somehow depends on the spring constant k and how much the string is stretched from its equilibrium position x. Then is has a form:

\(U_s=dk^ex^f\)      (9.3)

where d, e, and f are dimensionless numbers. Then the mechanical energy is:

\(E_{\rm mech}=\frac{1}{2}mv^2+dk^ex^f\)        (9.4)

You will determine the values of d, e, and f.

1. The unit of U_s must be energy, and the unit of the spring constant k is force/distance. What must be the values of e and f in Equation 9.4? Rewrite Equation 9.4 with these values of e and f.

2. If the mechanical energy is conserved what must be the value of \(\frac{dE_{\rm mech}}{dt}\) ? Explain.

3. Calculate \(\frac{dE_{\rm mech}}{dt}\) from the equation of Part A, and set the result equal to your answer to Part B. Compare to Eqn. 9.1 to determine the value of d. Is your result consistent with Eqn. 9.2?

 

   Activity 10

In Mechanics Module 2 Activity 9 you determined the angle with the horizontal, \(\theta\) , that the track must make if the cart is to roll down it with constant speed. You will need to use your data from Module 2 Activity 9 for this Activity.

As the cart rolls down the track is mechanical energy conserved?

If your answer is Yes, explain.

If your answer is No, where did the energy go? How much mechanical energy is lost if the cart travels 1 m down the track?

 

   Activity 11

Work is a word that is used both in Physics and in everyday life. Although the meanings of the word in these two contexts are similar, they are not identical. In 5 minutes or less think of as many uses as you can of the word work in your everyday life that do not correspond to the Physics definition, and illustrate each by using it in a complete sentence.

 

    Activity 12

The relation between the s component of a force acting on an object, F_s, and the potential energy U is:

(11.1)

Note the minus sign.

Here are some other equations from the textbook with minus signs:

Are any of these minus signs conceptually the same as the one that appears in Eqn. 11.1? Explain.

 

   Activity 13

As you may already know Leibniz, a contemporary and bitter rival of Newton, believed that the “vis viva” mv² was the most crucial concept for understanding mechanics. Newton believed that the momentum was the most important quantity.

1. Now, we usually use one-half of the vis viva, ½ mv², and call it the kinetic energy. In your own words describe how the factor of one-half arises in the definition of kinetic energy.

2. Who do you think was right about the most important quantity: Newton or Leibniz? Why?

 

    Activty 14 

You have a small, plastic toy with a suction cup attached to the bottom. There is also a spring attached to a black piece of plastic. If you put the toy on the spring and compress the spring, you can make them stick together for a short time. The suction will fail spontaneously and the toy will fly upward.  This is called a "jumper".

1. Use the force sensor and ruler to measure the spring constant, k, of the spring.  To do this, compress the spring by an amount you can easily measure, and, at the same time, measure the force change with the computer.  [You can find "Force Sensor" under "Labview Shortcuts".]
2. Measure the amount of compression of the spring, \(\Delta x\), when the jumper is fully compressed and ready to jump. (See image.)  This will probably be larger than the amount that you compressed the spring in part A. 

3. Combine  the spring constant you measured from part A with the compression amount you measured from Part B to estimate the initial energy stored in the spring: \(E_{spring}=\frac{1}{2}k(\Delta x)^2\)
4. Allow the jumper to jump, and measure the height, h, that it jumps.  To do this, you may wish to take a video using the Camera app on your computer. This video can be imported into the "Tracker" app which should be on your desktop.  You should set up a Calibration Stick, which is something at the same distance as the jumper in the video for which you know the length (ie a meter-stick).  Click Track and add a Point mass.  Frame by frame, press shift while you click the mouse button to add position-time measurements for the frames in which the projectile was in the air. 
5. Measure the mass of the jumper.  From this and the measured height, h, that the jumper jumps, estimate its change in gravitational energy as it goes from its minimum to its maximum height.  Compare the change in gravitational potential energy to the initial energy stored in the spring.  What fraction of the initial energy stored in the spring gets transferred to gravitational potential energy during the jump?  If the stored spring energy is greater than the gravitational potential energy, can you think of any other forms of energy where the remaining energy might have gone?

 

    Activity 15

 

Skills used in this activity. Able to extract the information from the representation.

Two equal mass blocks are initially at rest and sitting on a frictionless surface. A hand exerts a force of magnitude F on block A, which pushes it to the right by a distance d. Another hand exerts of force of the same magnitude F on block B, which pushes it to the left the same distance d.

1. Is the sign of the work the hand on the left does on block A positive, negative, or is it zero? Explain.

2. Is the sign of the work the hand on the right does on block B positive, negative, or is it zero? Explain.

3. Consider the blocks A and B as the system. Is the sign of the net external work done by the hands on the system positive, negative, or is it zero? Explain.

 

    Activity 16

Skills used in this activity. Able to extract the information from the representation.

Two equal mass blocks are initially at rest and sitting on a frictionless surface. The blocks are connected by a massless ideal spring that is initially at its equilibrium position. A hand exerts a force of magnitude F on block A, which pushes it to the right by a distance d. Another hand exerts of force of the same magnitude F on block B, which pushes it to the left the same distance d. Consider the blocks A and B and the spring as the system.

1. Is the sign of the net external work done by the hands on the system positive, negative, or is it zero? Explain.

2. Is the change in the total energy \(\Delta E_{tot}\) of the system positive, negative, or is it zero? Explain.

 

    Activity 17

 

A block is initially at rest on a frictionless surface. It is connected to a massless ideal spring which is stretched a distance d from its equilibrium position. The other end of the spring is fixed to a wall. The block is kept in place by a hand. The hand releases the block and it moves to the right. In the After figure, the spring is at its equilibrium position and the block is moving to the right with speed v. Consider the block and spring as "the system".

1. Within the system, the spring exerts a force on the block as it moves.  Is the sign of the work done by the spring on the block positive, negative, or is it zero?  Explain.

2. Within the system, the block exerts a force on the spring as it moves.  Is the sign of the work done by the block on the spring positive, negative, or is it zero?  Explain.

3. Is the sign of the work W done by the wall on the system positive, negative, or is it zero? Explain.

4. Is the sign of the work done by the system on the wall positive, negative, or is it zero?  Explain.

5. Is the change in the total energy  ​\(\Delta E_{tot}\)​ of the system positive, negative, or is it zero? Explain.

 

    Activty 18

 

1. Follow the instructions listed under Preparing for Activities 12-14 of Mechanics Module 1.

2. The track should be arranged so that the 0 cm position on the ruler is closest to the wall. Put a 1.000 cm thick block or metal plate under the feet of the track closest to the wall.

3. Place the cart at about 30 cm. Once released, it will travel to the lower  end of the track starting from rest. Do not allow the cart to crash and fall off of the track.

4. A motion sensor is a device that employs pulses of sound to find the position of an object. Further details about this device are given in Activity 10 of Mechanics Module 2. Place the sensor on the track closest to the wall. Be careful not to damage it. The switch on the top of the sensor should be on narrow beam which might be displayed as a picture of a cart. Rotate the sensor towards the cart and track.

5. Is the mechanical energy of the cart conserved as it travels along the track? Make quantitative measurements using the motion sensor and computer and the ruler. Explain your answer.

    Activity 19

 

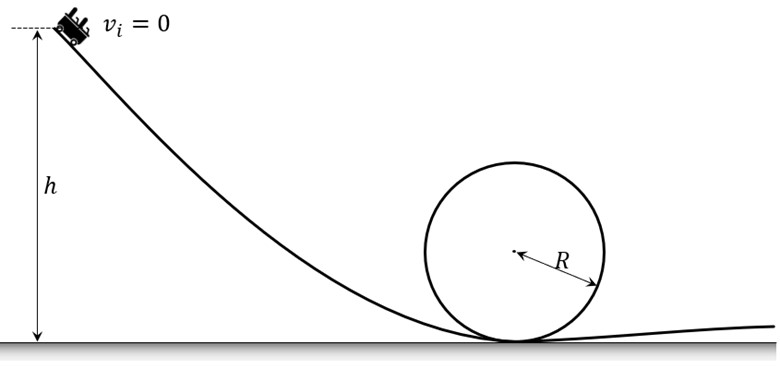
A roller coaster cart of mass m starts from rest at a height h above the ground, as shown.  It completes a loop-de-loop, going fully around the vertical circular path shown.  The cart is on wheels on the track, so there is only a regular Normal Force, pushing the wheels of the cart (not pulling).  What is the minimum initial height, h, needed so the cart remains in contact with the track the full way around the circle?  You may neglect friction and air resistance. Express your answer in terms of one or more of the following variables: m, g, R. 

 

 

 

This Student Guide was written by David M. Harrison, Dept. of Physics, Univ. of Toronto, in the Fall of 2008. Activity 3 is from Randall Knight, Student Workbook that accompanies the 1^st edition of Physics for Scientists and Engineers (Pearson Addison-Wesley, 2004), Section 10.3, Activity 10. Activity 14 is similar to Priscilla Laws et al., Workshop Physics Activity Guide (John Wiley, 2004), Unit 11, 11.7. Activities 15 – 17 are from Beth A. Lindsey Paula R. L. Heron, and Peter S. Shaffer, American Journal of Physics 77(11), November 2009, 999 – 1009.

Activity 18 from Vatche Deyirmenjian

Activity 19 from Jason Harlow